A Flexible Definition of sinθ and cosθ

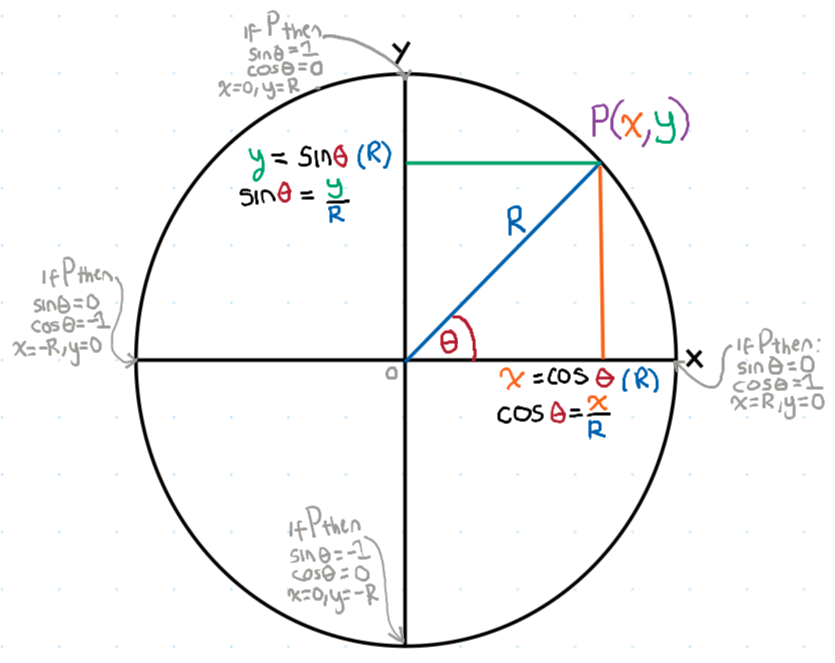
Imagine a point P moving on a circle of radius R centered at the origin of an x-y coordinate system. Let the angle θ be measured counterclockwise from the positive x-axis to the line segment connecting the origin to point P.

The coordinates of point P are given by (x, y).

Then, the cosine and sine of the angle θ are defined as the normalised coordinates of this point:

• cos(θ) = x / R (The ratio of the horizontal coordinate to the radius)
• sin(θ) = y / R (The ratio of the vertical coordinate to the radius)

This definition is flexible:

• You can treat the Unit Circle definition as a special case: If you choose R=1, this simplifies to cos(θ) = x and sin(θ) = y.
• Because x and y are coordinates, they can be positive or negative, naturally defining sine and cosine in all four quadrants and for angles beyond 360° or negative angles.
• It supports the SOH CAH TOA definition: for 0 < θ < 90°, you can draw a right triangle with x as the adjacent side, y as the opposite side, and R as the hypotenuse.
• Defining it with radius R makes it applicable to physical situations where the magnitude is not 1 (e.g., the length of a link in a robot).