1 Rotating \(\vec{v}\)
Consider the following two-dimensional (2D) vector \(\vec {v}\) in the 2D plane. We can rotate vector \(\vec{v}\) by an angle \(\theta\) to produce \(\vec{v}'\):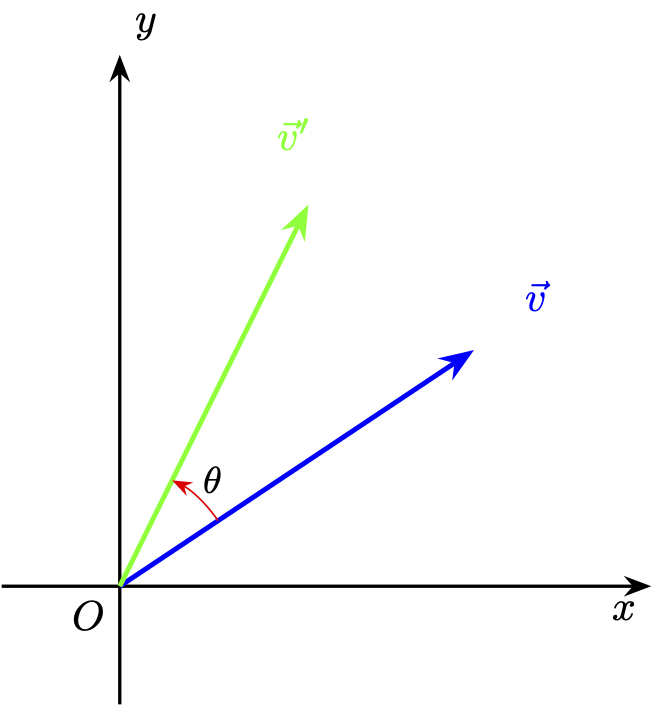
In this article, we will derive the 2D rotation matrix \(R(\theta)\), which rotates vectors counter-clockwise for positive angles \(\theta\), and clockwise for negative angles \(\theta\).
Recall that vector \(\vec{v}\) is the sum of two component vectors: \[ \vec {v} = \vec{v}_x + \vec{v}_y \]
Where each component vector is a scaled basis vector:
\[
\vec{v}_x = x\hat{i} = x\begin{bmatrix} 1\\0 \end{bmatrix} = \begin{bmatrix} x \\0 \end{bmatrix}
\] \[
\vec{v}_y = y\hat{j} = y\begin{bmatrix} 0\\1 \end{bmatrix} = \begin{bmatrix} 0 \\y \end{bmatrix}
\] To rotate \(\vec{v}\) by angle \(\theta\) to produce \(\vec{v}'\) we sum the rotated component vectors:
\[
\vec{v}' = \vec{v}'_x + \vec{v}'_y
\]
Visualise the rotation of the two component vectors:
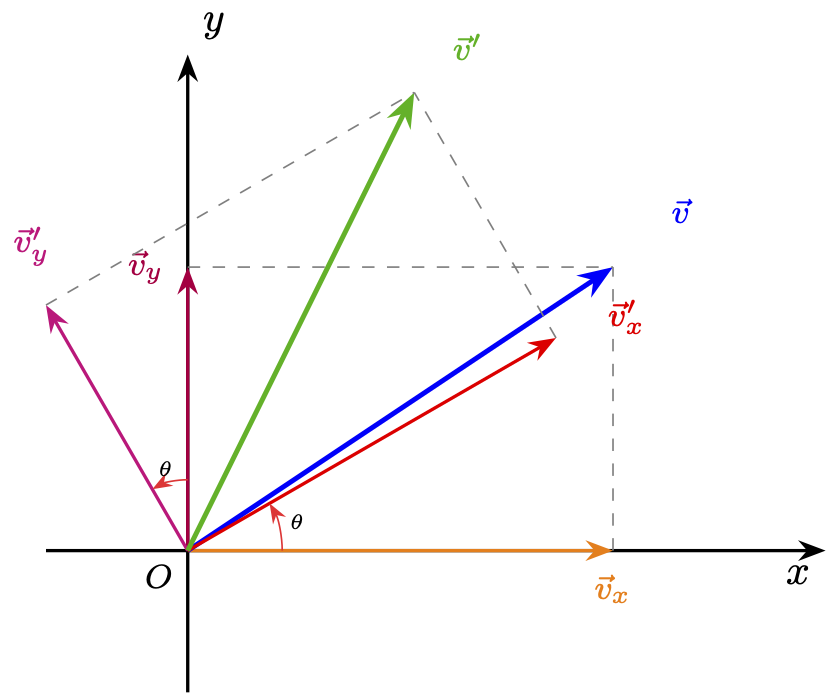
2 Determine \(\vec{v}'_x\)
Rotating \(\vec{v}_x\) by \(\theta\) produces \(\vec{v}'_x\). The length of \(\vec{v}_x\) is: \[ ||\vec{v}_x|| = \sqrt[]{x^2 + 0^2} = |x| \] This length is preserved during rotation, so the magnitude of \(\vec{v}'_x\) is also \(|x|\). This length forms the hypotenuse of the right-angled triangle created by \(\vec{v}'_x\) and the axes:
\[ hyp = |(\vec{v}_x)_0| = |x| \]
Recall that in a right-angled triangle, the cosine of an angle is equal to the length of the adjacent side divided by the length of the hypotenuse: \[ \cos (\theta) = \frac{adj}{hyp} \] Hence, we can calculate the \(x\)-coordinate of \(\vec{v}'_x\) as follows: \[ (\vec{v}'_x)_0 = \cos (\theta) x \]
Note that we use \(x\) (not \(∣x∣\)) in the formula \(\cos(\theta)x\); the sign of \(x\) correctly orients the resulting component. We follow the same practice for \(y\) later.
Recall that in a right-angled triangle, the sine of an angle is equal to the length of the opposite side divided by the length of the hypotenuse: \[ \sin (\theta) = \frac{opp}{hyp} \] We can again use the fact that the absolute value of the first element of \(\vec{v}_x\) is equal to the length of the hypotenuse to calculate the \(y\)-coordinate of \(\vec{v}'_x\): \[ (\vec{v}'_x)_1 = \sin (\theta)x \] \(\vec{v}'_x\) in full: \[ \vec{v}'_x = \begin{bmatrix} (\vec{v}'_x)_0 \\ (\vec{v}'_x)_1 \end{bmatrix} = \begin{bmatrix} \cos(\theta) x \\ \sin(\theta) x \end{bmatrix} \]
Visualise the use of \(x \cos \theta\) and \(x \sin \theta\):
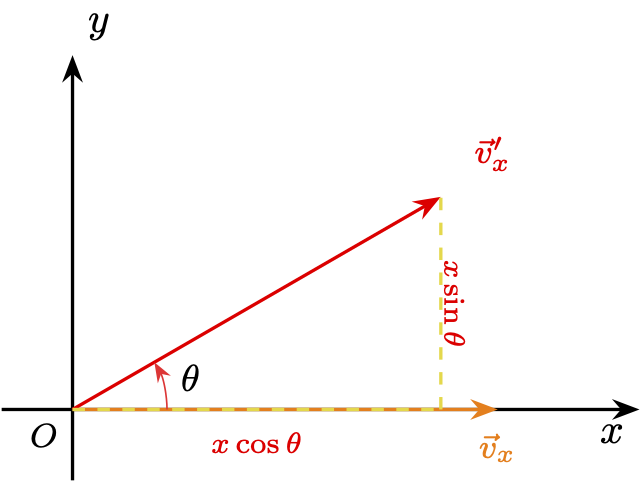
3 Determine \(\vec{v}'_y\)
Rotating \(\vec{v}_y\) by \(\theta\) produces \(\vec{v}'_y\). The length of \(\vec{v}_y\) is:
\[ ||\vec{v}_y|| = \sqrt[]{0^2 + y^2} = |y| \]
This length is preserved during the rotation, so the magnitude of \(\vec{v}'_y\) is also |y|. This length forms the hypotenuse of the right-angled triangle created by \(\vec{v}'_y\) and the axes:
\[ hyp = |(\vec{v}_y)_1| = |y| \]
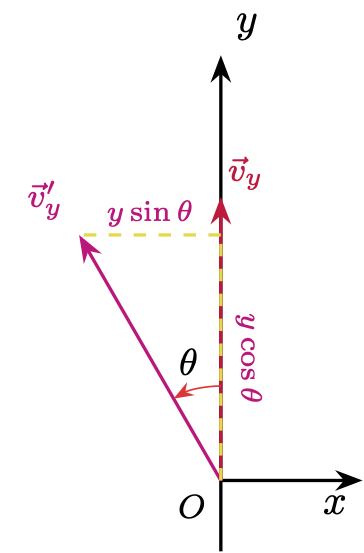
Calculate the \(x\)-coordinate of \(\vec{v}'_y\): \[ (\vec{v}'_y)_0 = -(\sin(\theta)y) \] Note that because this rotation moves the tip of \(\vec{v}_y\) to the left, into the negative \(x\) direction, we multiply its contribution by -1; consult the following diagram for a visual aid:
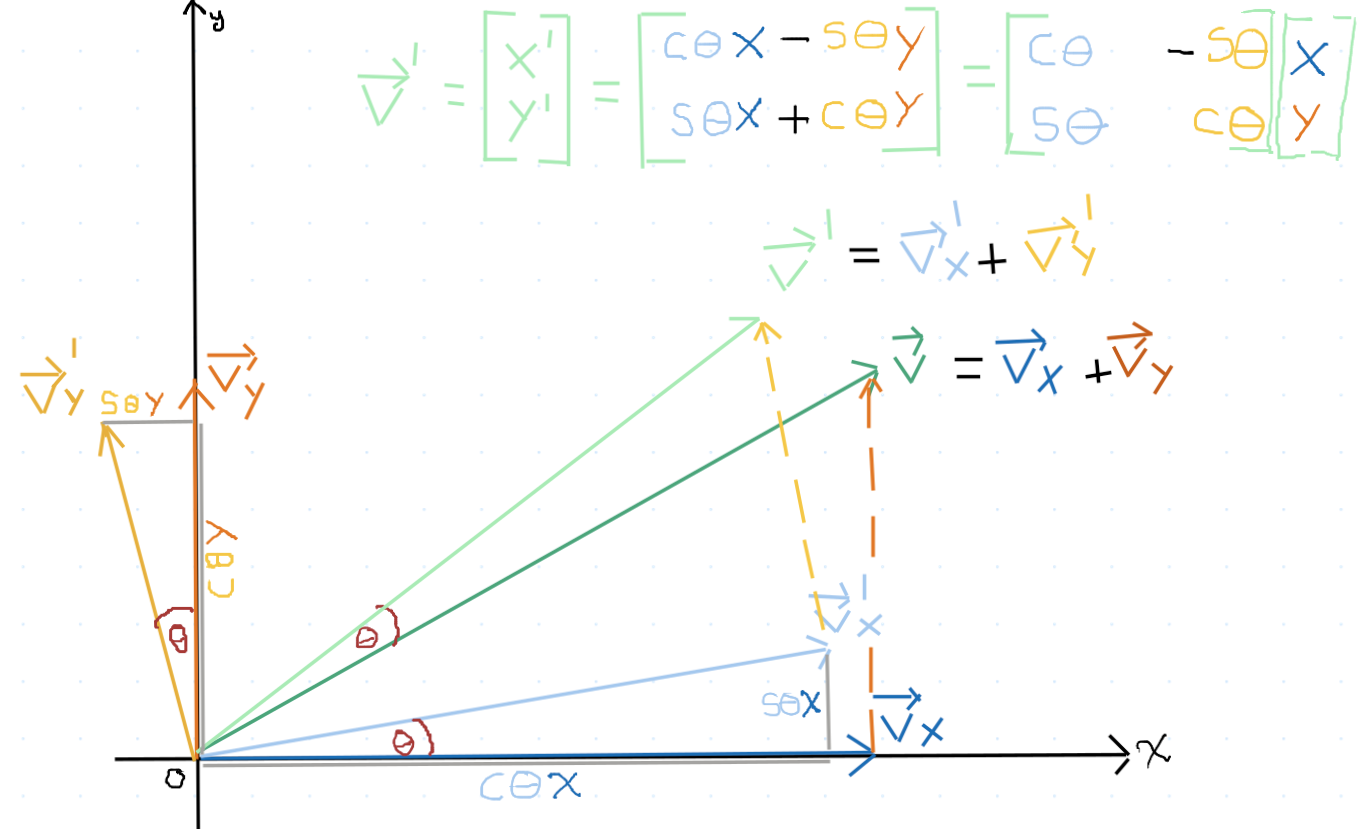
Next, calculate the the \(y\)-coordinate of \(\vec{v}'_y\): \[ (\vec{v}'_y)_1 = \cos(\theta)y \] \(\vec{v}'_y\) in full: \[ \vec{v}'_y = \begin{bmatrix} (\vec{v}'_y)_0 \\ (\vec{v}'_y)_1 \end{bmatrix} = \begin{bmatrix} -\sin(\theta)y \\ \cos(\theta)y \end{bmatrix} \]
Visualise the use of \(y \cos \theta\) and \(y \sin \theta\):
4 Derive \(R(\theta)\):
Calculate the rotated vector by summing the rotated components:
\[ \vec{v}' = \vec{v}'_x + \vec{v}'_y = \begin{bmatrix} \cos(\theta)x \\ \sin(\theta)x \end{bmatrix} + \begin{bmatrix} -\sin(\theta)y \\ \cos(\theta)y \end{bmatrix} = \begin{bmatrix} \cos(\theta)x - \sin(\theta)y \\ \sin(\theta)x + \cos(\theta)y \end{bmatrix} \]
Recall the definition of multiplying a 2x2 matrix by a 2x1 vector: \[ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix} \]
Recognise that we can express \(\vec{v}'\) as a matrix multiplication: \[ \vec{v}' = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \]
We have now derived the 2D rotation matrix \(R(\theta)\): \[ R(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \]
This matrix allows us to rotate any 2D vector \(\vec{v} = \begin{bmatrix} x \\ y \end{bmatrix}\) by an angle \(\theta\) (counter-clockwise for positive \(\theta\), clockwise for negative \(\theta\)) by performing the matrix multiplication \(\vec{v}' = R(\theta)\vec{v}\).
5 \(R(\theta)\) in Python
The following Python code implements matrix multiplication between the 2D rotation matrix we just derived and a 2D vector to rotate the vector by the specified number of degrees:
import math
class Vec2D:
def __init__(self, x: float, y: float):
self.x = x
self.y = y
def __repr__(self):
return f"Vec2D(x={round(self.x, 2)}, y={round(self.y, 2)})"
class R:
def __init__(self, degrees: float):
radians = degrees*(math.pi/180)
self.cosθ = math.cos(radians)
self.sinθ = math.sin(radians)
def __mul__(self, other) -> Vec2D:
if isinstance(other, Vec2D):
return Vec2D(
x=self.cosθ*other.x - self.sinθ*other.y,
y=self.sinθ*other.x + self.cosθ*other.y
)
else:
return NotImplemented
print(R(degrees=20) * Vec2D(x=7, y=4))
# Vec2D(x=5.21, y=6.15)
print(Vec2D(x=7, y=4) * R(degrees=20))
# TypeError: unsupported operand type(s) for *: 'Vec2D' and 'R'